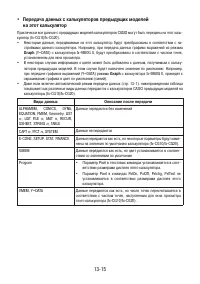
Калькуляторы Casio FX-CG20 - инструкция пользователя по применению, эксплуатации и установке на русском языке. Мы надеемся, она поможет вам решить возникшие у вас вопросы при эксплуатации техники.
Если остались вопросы, задайте их в комментариях после инструкции.
"Загружаем инструкцию", означает, что нужно подождать пока файл загрузится и можно будет его читать онлайн. Некоторые инструкции очень большие и время их появления зависит от вашей скорости интернета.

6-17
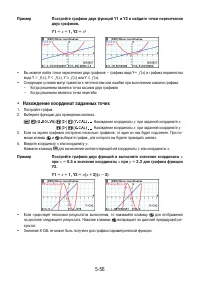
График линейной регрессии при наличии экстремальных
значений
Если предполагается наличие ряда экстремальных значений, то вместо метода наименьших квадратов
можно использовать метод построения линейного графика с экстремальными значениями. Этот метод
аналогичен линейной регрессии, но позволяет минимизировать влияние экстремальных значений.
Ниже приведен вид формулы линейной регрессии с экстремальными значениями.
y
=
ax
+
b
a
.......... коэффициент регрессии (угловой коэффициент)
b
.......... постоянный член регрессии (координата
y
при
x
= 0)
Графики регрессий второго/третьего/четвертого порядков
Графики уравнений второго/третьего/четвертого порядков представляют собой кривую, проходящую
максимально близко к точкам данных. Для построения таких кривых используется метод наименьших
квадратов. Формула, на основании которой строятся графики, и является регрессией второго/третьего/
четвертого порядков.
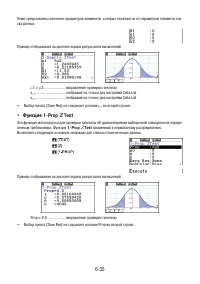
Пример
Регрессия второго порядка
Регрессия второго порядка
Регрессия третьего порядка
Формула вида .......
y
=
ax
2
+
bx
+
c
Формула вида .......
y
=
ax
3
+
bx
2
+
cx
+
d
a
................. второй коэффициент регрессии
a
.................. третий коэффициент регрессии
b
.................. первый коэффициент регрессии
b
.................. второй коэффициент регрессии
c
.................. постоянный член регрессии
c
.................. первый коэффициент регрессии
(координата
y
при
x
= 0)
d
.................. постоянный член регрессии
(координата
y
при
x
= 0)
Регрессия четвертого порядка
Формула вида .......
y
= ax
4
+ bx
3
+ cx
2
+ dx + e
a
................. четвертый коэффициент регрессии
b
.................. третий коэффициент регрессии
c
.................. второй коэффициент регрессии
d
................. первый коэффициент регрессии
e
.................. постоянный член регрессии (координата
y
при
x
= 0)